전치 행렬은 열 벡터 및 행 벡터 변환, 이미지 프로세싱에서 사진 변환 등 다양한 곳에서 사용되고 있는 행렬입니다.

전치 행렬(Transposed Matrix): 열과 행을 바꾼 행렬
즉, i * n 행렬 A = [Mij]를 [Mji]로 바꾼 행렬
- 전치 행렬 예시
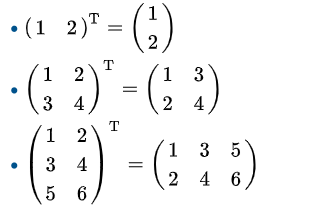
전치 행렬의 성질
전치 행렬은 다음과 같은 특징을 지닙니다.
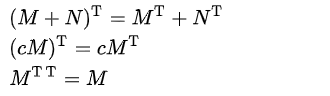
- 행렬의 곱의 전치
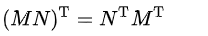
- 전치 행렬과 행렬식
임의의 행렬과 그 전치행렬의 행렬식 값은 동일!
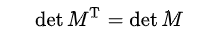
- 전치 행렬과 역행렬
임의의 행렬이 가역성을 가지면 전치 행렬 역시 가역성을 가짐
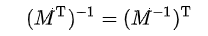
만약 임의의 i, j (i,j = 1, 2, ..., n)에 대해서 a(i,j) = a(j,i) 이 성립한다면 전치하여도 기존의 행렬과 전치행렬이 같을 것입니다.
이를 대칭행렬(Symmetric Matrix)라고 합니다.

[출처] 행렬(Matrix) - 전치 행렬(Transposed Matrix)이란?|작성자 예비개발자
개발자의 개발 정보와 리뷰 : 네이버 블로그
안녕하세요. AI/ML 개발자 '예비개발자'입니다! 개발자분들에게 많은 도움이 되는 블로그가 되었으면 좋겠네요 :)
blog.naver.com
https://datalabbit.tistory.com/37
[행렬대수학] 전치행렬(Transposed Matrix)
안녕하십니까, 간토끼입니다. 이번 포스팅에서는 전치행렬(Transposed Matrix)의 개념에 대해서 다뤄보겠습니다. 전치행렬이란 임의의 행렬 A가 주어졌을 때, 그 행렬의 행과 열을 바꾸어 얻어낸 행
datalabbit.tistory.com
'수학 > 행렬' 카테고리의 다른 글
| 역행렬과 행렬 곱셈의 성질 (0) | 2023.02.27 |
|---|---|
| 단위행렬 (0) | 2023.02.24 |
| 행렬 곱셈의 크기 (0) | 2023.02.24 |
| 행렬 스칼라 곱셈의 성질 (0) | 2023.02.24 |
| 행렬 덧셈의 성질 (0) | 2023.02.24 |

