역행렬
행렬의 곱셉에 대한 역원을 의미한다.
임의의 정사각행렬 A
곱셈에 대한 역원 A-1을 역행렬이라고 한다.
한 행렬에 대하여 역행렬은 하나 뿐이다.
A * A-1 = I
즉, 행렬과 해당 행렬의 역행렬의 곱은 단위행렬이 된다.
A 가 2X2 정사각행렬일 때 기준 A-1 역행렬은
= 1/ad-bc *
| d | -b |
| -c | a |
이다.
따라서 ad-bc 가 0 이면 분모가 0이므로 역행렬이 존재하지 않는다.
행렬 곱셈의 성질
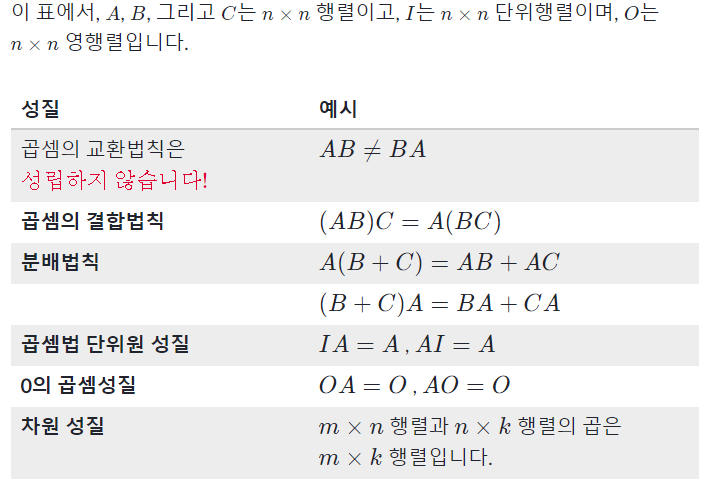
중요한 점은 곱셈의 교환법칙이 성립하지 않는다는 것이다!
출처 :
행렬 스칼라 곱셈의 성질 (개념 이해하기) | 행렬 | Khan Academy
수학, 예술, 컴퓨터 프로그래밍, 경제, 물리학, 화학, 생물학, 의학, 금융, 역사 등을 무료로 학습해 보세요. 칸아카데미는 어디에서나 누구에게나 세계 최고의 무료 교육을 제공하는 미션을 가진
ko.khanacademy.org

