내적
일반적 정의 :
두 벡터의 각 성분끼리의 곱의 합
두 개의 벡터가 있을때 한 벡터의 방향으로 나머지 하나를 projection(투영) 시킨 것과 다른 한 벡터의 크기의 곱
내적 연산은 벡터 두 개를 하나의 스칼라 값으로 변환시키는 연산
벡터의 내적은 두 벡터의 각 성분끼리의 곱의 합으로 정의한다.
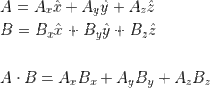
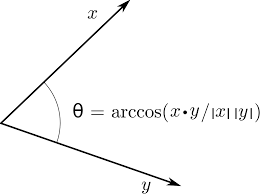
두 벡터가 이루는 각의 크기를 세타라고 한다면 벡터의 내적은 다음과 같이 정의한다. (정의.2)
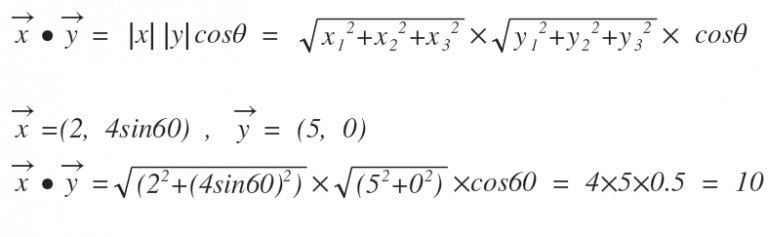
(정의.1)과 (정의.2)에 따라 두 벡터의 좌표가 주어지면, 두 벡터간의 사잇각을 알 수 있다.
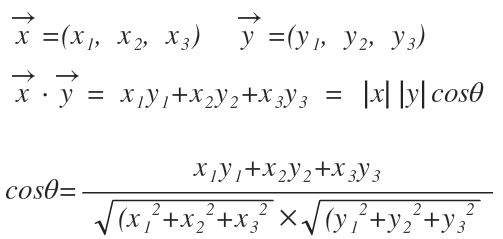
내적(inner product)
두 벡터의 사이각을 알아내는데 유용하다
내적은 스칼라곱(scalar product) 또는 dot product라고도 말하며, 두 벡터의 크기와 두 벡터 사이의 각의 코사인 값을 곱한것으로 정의한다. (결과는 스칼라양이 나온다) 수식으로 적어보면,
A*B = |A||B|cosθ
그리고 단위벡터를 이용하면 다른 방법으로 내적을 구할 수 있다.
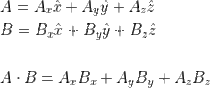
cos(θ) = a · b 로 간략화 한다면
a · b벡터의 연산은 성분끼리 곱하면 됩니다.
θ = (a_x * b_x) + (a_y * b_y);
내적 (Inner Product)
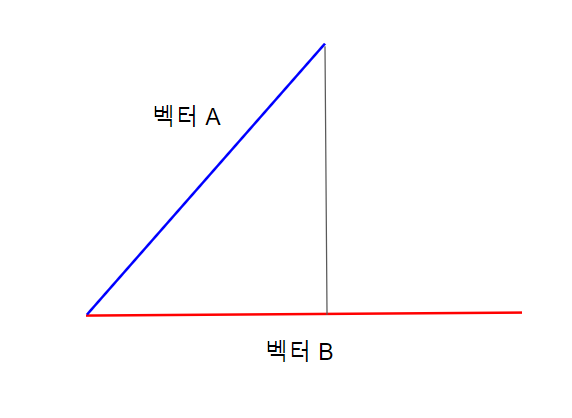
내적은 두 벡터의 곱이라고 생각할 수 있습니다. 그래서 Dot Product라고 부르고, 수학적으로 · 이란 기호를 사용합니다. 벡터 A와 벡터 B의 내적은 A · B 로 표현할 수 있습니다. 이를 좀 더 풀어서 표현하면 A · B = |A| |B| Cosθ 로 표현이 가능합니다. 여기서 |A| 는 벡터 A의 크기이고 θ는 벡터 A, B 사이에 이루는 각도입니다.
여기서 |A|Cosθ는 벡터 B와 평행하고 벡터 A에서 벡터 B로 수직으로 그은 삼각형의 밑변이 됩니다. 따라서 여기에 |B|를 곱하면 내적이 되는 것입니다.
일반적으로 벡터는 2차원이나 3차원에서만 해당되는 이야기가 아닙니다. 차원이 올라가서 n 차원이 되더라도 유클리드 공간에서는 성립하는 공식이 됩니다. 이제 공식과 같이 기억을 하고 있으면 좋은 것이 있는데요. 두 벡터가 수직일때 내적은 계산하나마나 0 이 된다 입니다. 그 이유는 Cosθ 가 θ 가 90인 경우 0이기 때문입니다.
외적은 두 벡터의 수직인 벡터를 구하는 방법입니다. 기호로 x 를 사용하고 A x B 로 표현합니다. 일반적으로 외적 혹은 cross product라고 불리는데요. A x B 를 하면 두 벡터에 수직인 새로운 벡터 C가 나오기 때문에 수학적으로 표현하면 A x B = C 가 됩니다.
외적 (outer product)
두 벡터의 벡터곱(vector product, cross product)의 결과는 벡터인 반면에, 두 벡터의 외적(outer product)의 결과는 행렬입니다. 두 벡터의 외적(outper product)은 아래와 같이 계산합니다.



출처 :
벡터의 곱셈(내적과 외적)
벡터의 곱셈에는 내적과 외적이 있다. 1. 내적(inner product) 내적은 벡터의 특정 방향, 성분, 투영(사영)...
blog.naver.com
https://math-development-geometry.tistory.com/45
벡터의 외적(Cross Product)과 내적(Inner Product)
벡터는 컴퓨터 그래픽과 기하학에서 모두 중요한 내용입니다. 우선 벡터가 무엇인지 알아보도록 하겠습니다. 어떤 사람이 앞으로 걸어가고 있습니다. 그 사람의 위치는 시간이 지나면 변하게
math-development-geometry.tistory.com
https://rfriend.tistory.com/146
R (7) 벡터의 곱 - [2] 벡터곱 (cross product, vector product), 외적(outer product)
지난번 포스팅에서 벡터의 곱 첫번째로 내적 (inner product, dot product, scalar product, projection product)에 대해서 알아보았습니다. 이번에는 벡터의 곱 두번째로 벡터곱(vector product, cross product)과 외적 (out
rfriend.tistory.com
벡터의 내적과 외적 기본 계산 공식
예제 ) A = 2i - 3j - k, B = i + 4j - 2k 두 벡터의 내적과 외적을 구하시오. (i, j, k는 x,y,z 축의 단위벡터. i = (1,0,0) ) 내적은 x,y,z 좌표끼리 곱하기만 하면 되므로, 2x1 + (-3 ) x 4 + (-1) x (-2) = 2 - 12 + 2 = -8 외
2srin.tistory.com
'수학 > 벡터' 카테고리의 다른 글
| 벡터의 곱연산 (0) | 2023.03.05 |
|---|---|
| 벡터의 합연산 (0) | 2023.03.05 |
| 벡터의 길이 스칼라 (0) | 2023.03.05 |
| 단위 벡터 (0) | 2023.02.27 |
| 벡터와 스칼라의 곱셈 (0) | 2023.02.27 |



