벡터곱의 정의 (definition of vector product)
두 벡터 a와 b에 모두 수직이 되는 벡터로서, v와 수직이 되는 두 벡터 a와 b는 공간 속의 평면 위에 있는 한 평행사변형의 두 변을 이루게 되며, 그 벡터의 길이(힘의 크기) |v|는 평행사변형의 면적과 같습니다.
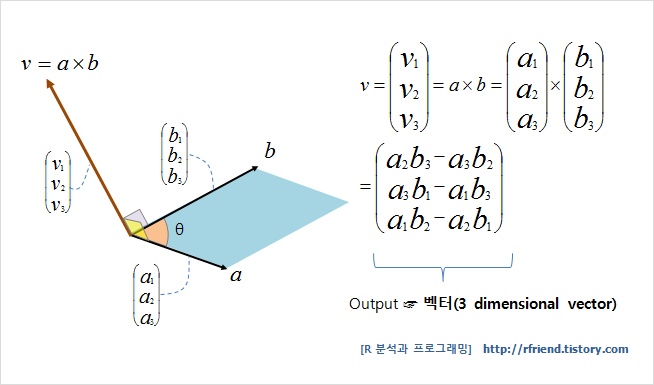
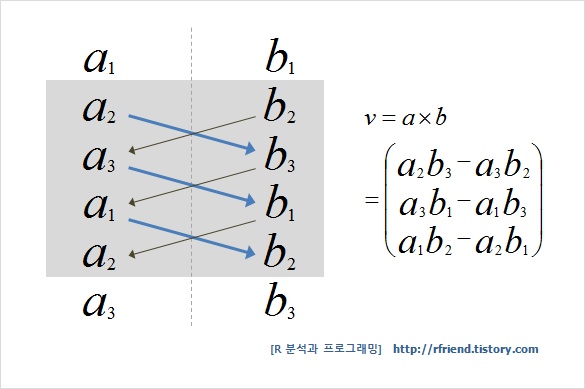
벡터곱 계산을 쉽게 기억하는 방법 (easy way to memorize vector product calculation)
내적 대비 벡터곱 계산하는 방법이 많이 어려워보일 수 있는데요, 아래처럼 벡터 a와 b의 component를 두번씩 세로로 써 놓고 두번재째 행부터 순차적으로 대각선으로 곱하고 빼나가면 v1, v2, v3를 구할 수 있습니다.
두 벡터로 이루어진 평행사변형의 넓이 계산 (calculation of the area of the parallelogram spanned by vector a and b)
두 벡터 a와 b의 벡터곱(vector product, cross product)은 두 벡터로 이루어진 평행사변형의 넓이와 같다고 하였습니다. 두 벡터 a와 b로 이루어진 평행사변형의 넓이를 구해보면 (6)번에서 제시한 두 벡터의 벡터곱 공식과 일치함을 알 수 있습니다. 두 벡터로 이루어진 평행사변형의 넓이를 구하고 싶으면 두 벡터의 벡터곱을 구하면 되겠습니다.

벡터곱의 성질 (properties of vector product)
벡터곱은 내적과 같은 성질도 있고 다른 성질도 있습니다. 임의의 실수와의 곱은 순서에 상관없이 모두 동일하다는 점과 분배법칙(distributive law)을 만족한다는 점은 내적과 벡터곱이 동일합니다.
반면에 내적은 교환법칙(commutative law)이 성립하지만, 벡터곱은 교환법칙이 성립하지 않는다(anti-commutative)는 점에서 차이가 있습니다. 그리고 벡터곱은 결합법칙도 일반적으로 성립하지 않는다(not associative)는 점 때문에 괄호를 생략하면 안됩니다. 내적은 결과가 scalar 이지만 벡터곱은 결과가 vector이므로 서로 다른 성질을 가지게 되는 것입니다.

출처 :
https://rfriend.tistory.com/146
R (7) 벡터의 곱 - [2] 벡터곱 (cross product, vector product), 외적(outer product)
지난번 포스팅에서 벡터의 곱 첫번째로 내적 (inner product, dot product, scalar product, projection product)에 대해서 알아보았습니다. 이번에는 벡터의 곱 두번째로 벡터곱(vector product, cross product)과 외적 (out
rfriend.tistory.com
'수학 > 벡터' 카테고리의 다른 글
| 내적과 외적 (0) | 2023.03.05 |
|---|---|
| 벡터의 합연산 (0) | 2023.03.05 |
| 벡터의 길이 스칼라 (0) | 2023.03.05 |
| 단위 벡터 (0) | 2023.02.27 |
| 벡터와 스칼라의 곱셈 (0) | 2023.02.27 |



