이진트리 : 각 노드가 최대 2개의 자식 노드를 가지는 트리
한개여도 되고 전부 공노드여도 괜찮다.
이진 트리는 특히 이진 트리 검색에서 많이 사용됨.
다만, 이진 검색 트리는 왼쪽 노드는 부모 노드보다 값이 작아야하고 오른쪽 노드는 부모 노드보다 값이 커야한다.

자식 노드 기준만이 아니라 아래 계층의 모든 노드가 해당 좌우 규칙을 지켜야한다.
트리는 구현 자
체에 난이도가 있다.
아래도 이진 검색 트리가 맞긴하지만….. 검색의 효율이 원하는 정도로 나오지않을것이다.
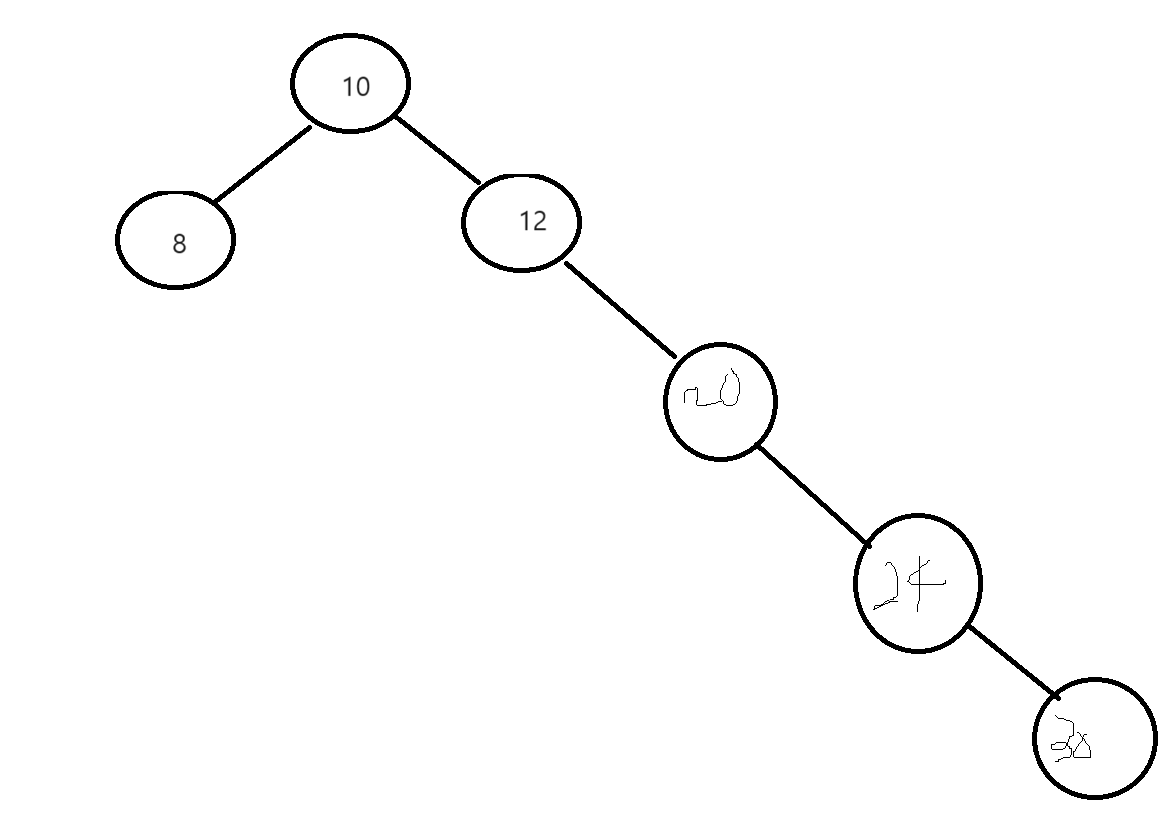
이때, 트리 재배치로 균형을 맞춰줘야한다. 이 방식이 AVL, 레드블랙트리 이다.
이진 검색 트리는 추가 삽입 삭제 난이도가 상당하다.
힙 트리 특징
이진 트리 기반이다.
- 부모 노드가 가진 값은 항상 자식 노드가 가진 값보다 크다
- 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있다.(완전 이진 트리)
- 마지막 레벨에 노드가 있을 때는, 항상 왼쪽부터 순서대로 채운다.
- 2,3 번을 통해서 노드 개수를 알면, 트리 구조는 무조건 확정할 수 있다.
힙 트리를 배열로 표현 할 때
- n 번 노드의 왼쪽 자식은 (2*n)+1 번 째 노드이다
- n 번 노드의 오른쪽 자식은 (2*n) + 2 번 째 노드이다
- n 번 노드의 부모 노드는 (n-1)/2 번째 노드이다.
힙트리에서 값 추가 시
- 먼저 마지막 레벨에 노드가 있을 때는, 항상 왼쪽부터 순서대로 채운다. 방식을 이용해서 노드를 먼저 추가한다.
- 생성된 노드를 레벨을 한 단계씩 높이면서 스왑을 한다!
- 스왑은 데이터의 우선순위를 기준으로 더 높은 순위이면 스왑 해준다.
- 더 이상 스왑이 불가능하면 힙트리에 값 추가 완료이다.
힙트리에서 최댓값 꺼내기
힙트리 개념은 루트 노드만 가져가는 개념이다.
중간 삭제를 위한 자료구조가 아니다!
- 일단 루트 노드 빼서 해당 데이터 잘쓴다~!
- 루트 노드가 비어 있는 상황이니 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있다.(완전 이진 트리) 이 규칙을 지켜야 한다.
- 따라서, 마지막 레벨의 마지막 노드를 루트 노드로 설정한다. (루트 노드 위치로 옮겨 버림)
- 그 후, 루트 노드로 간 마지막 노드(였던 것) 가 자식 노드 와 비교를 시작한다.
- 이때, 좌우 자식 노드 중 더 우선순위가 큰 것과 마지막 노드(였던 것)를 비교하고 순위가 밀리면 스왑하여 밀어낸다
- 순위가 밀리지 않을 때까지 가면 최댓값 도출 후 정리 성공
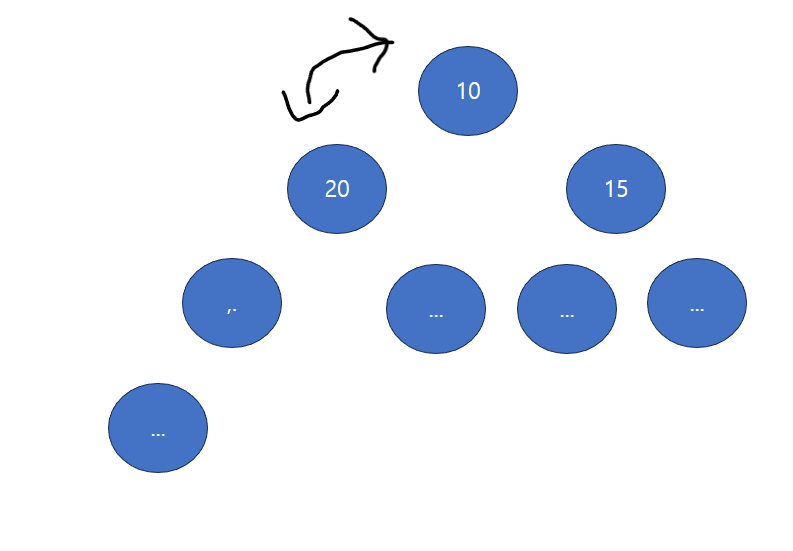
시간 복잡도 O(logn) 으로 굉장히 빠르다.
'자료구조 알고리즘' 카테고리의 다른 글
| 이진 탐색 트리 (0) | 2024.05.29 |
|---|---|
| 힙으로 구현한 우선순위 큐 (0) | 2024.05.29 |
| 트리 (0) | 2024.05.29 |
| BFS 인접 행렬 (0) | 2024.05.29 |
| BFS 인접 리스트 (0) | 2024.05.29 |


