이진 탐색 트리
이진 탐색을 배열로 실행하면 탐색 자체는 O(logn) 의 시간으로 빠른 탐색이 가능하지만 해당 배열에 삽입/삭제 시에는 결국 배열로 시간복잡도 O(n) 의 느린 삽입/삭제를 보인다.
삽입/삭제 또한, 빠르게 가능한 이진 탐색 트리를 알아본다.
이진 탐색 트리
이분 탐색 뿐만 아니라 삽입/삭제도 O(logn) 의 빠른 시간 복잡도를 가지는 트리 구조이다.
다만, 삽입 시 정렬된 수열이 차례로 삽입 되면 트리가 한 쪽으로 몰려서
탐색, 삽입, 삭제 시간 복잡도 O(n) 의 안좋은 경우가 생긴다.
이것을 위해 균형 이진 트리가 만들어짐
1. 부모노드의 왼쪽 자식노드는 부모 노드보다 작아야하며 오른쪽 자식 노드는 부모 노드보다 커야한다.
2. 위의 1번 규칙은 부모노드의 자식 노드 뿐 아니라 해당 부모노드의 아래 계층의 모든 노드에게 1번 규칙이 적용 되어야한다.
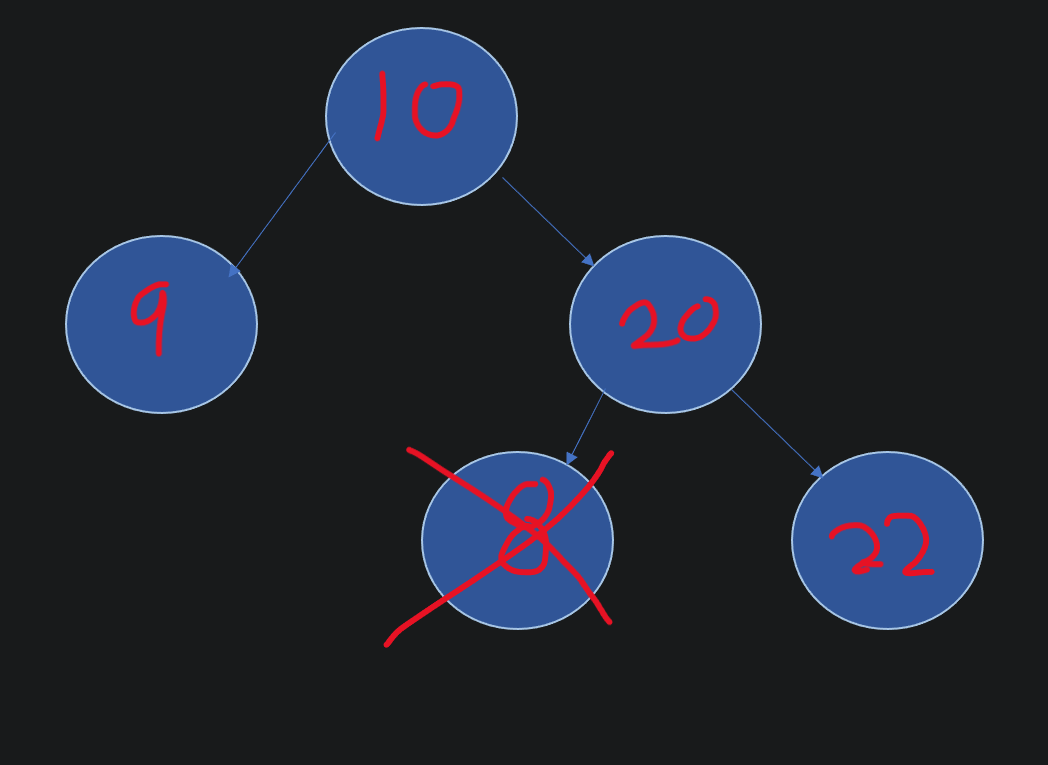
이진 탐색 트리의 순회 탐색에는 3가지 방법이 있다.
전위 순회
- 입력으로 들어온 현재 노드를 출력
- 왼쪽 노드 방문
- 오른쪽 노드 방문
중위 순회
- 왼쪽 노드를 방문
- 현재 노드를 출력
- 오른쪽 노드를 방문
후위 순회
- 왼쪽 노드 방문
- 오른쪽 노드 방문
- 현재 노드 출력
전 : 출력이 맨 앞
중 : 출력이 중간
후 : 출력이 맨 뒤
BST 코드
헤더 파일
#pragma once
#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <queue>
using namespace std;
// BST
// 부모 노드의 자식 노드는 왼쪽 자식노드는 부모 노드보다 작아야하며
// 오른쪽 자식 노드는 부모 노드보다 커야한다.
struct NodeTree
{
NodeTree* parent = nullptr;
NodeTree* left = nullptr;
NodeTree* right = nullptr;
int key = {};
// 더미 노드를 이용하여 관리 할 수도 있다.
bool external;
};
class BinarySearchTree
{
public:
void Print() { Print(_root, 10, 0); }
void Print(NodeTree* node, int x, int y);
void Print_Inorder() { Print_Inorder(_root); }
// 스캔
void Print_Inorder(NodeTree* node);
// 탐색 및 반환
NodeTree* Search(NodeTree* node, int key);
NodeTree* SearchWhile(NodeTree* node, int key);
NodeTree* Min(NodeTree* node);
NodeTree* Max(NodeTree* node);
NodeTree* Next(NodeTree* node);
// 키 값에 해당 하는 노드를 만들어서 트리에 삽입
void Insert(int key);
// 가장 복잡함
void Delete(int key);
void Delete(NodeTree* node);
void Replace(NodeTree* u, NodeTree* v);
public:
NodeTree* _root = nullptr;
};
소스 코드
#include "BinarySearchTree.h"
#include <Windows.h>
void SetCursorPosition(int x, int y)
{
HANDLE output = ::GetStdHandle(STD_OUTPUT_HANDLE);
COORD pos = { static_cast<SHORT>(x), static_cast<SHORT>(y) };
::SetConsoleCursorPosition(output, pos);
}
void BinarySearchTree::Print(NodeTree* node, int x, int y)
{
if (node == nullptr)
return;
SetCursorPosition(x, y);
cout << node->key;
Print(node->left, x - (5 / (y + 1)), y + 1);
Print(node->right, x + (5 / (y + 1)), y + 1);
}
void BinarySearchTree::Print_Inorder(NodeTree* node)
{
// 전위 순회 (preorder traverse)
// 중위 순회 (inorder)
// 후위 순회 (postorder)
// [중]
// [좌][우]
if (node == nullptr)
return;
Print_Inorder(node->left);
Print_Inorder(node->right);
cout << node->key << endl;
}
NodeTree* BinarySearchTree::Search(NodeTree* node, int key)
{
// 한 경로의 마지막 계층의 자식노드 즉 공노드가 나오거나
// 찾거나 (없거나 찾거나)
if (node == nullptr || key == node->key)
return node;
if (key < node->key)
return Search(node->left, key);
else
return Search(node->right, key);
}
NodeTree* BinarySearchTree::SearchWhile(NodeTree* node, int key)
{
while (node != nullptr && key != node->key)
{
if (key < node->key)
{
node = node->left;
}
else
{
node = node->right;
}
}
// 아예 없을 경우
return node;
}
NodeTree* BinarySearchTree::Min(NodeTree* node)
{
while (node->left)
node = node->left;
return node;
}
NodeTree* BinarySearchTree::Max(NodeTree* node)
{
while (node->right)
node = node->right;
return node;
}
NodeTree* BinarySearchTree::Next(NodeTree* node)
{
// 그냥 나보다 큰 애중에 가장 작은거 찾기
if (node->right)
return Min(node->right);
// 나보다 큰 친구가 나의 계층이 아닌 옆 계층에 존재할 때
NodeTree* parent = node->parent;
// 만약 내가 부모 노드의 왼쪽 자식이면 부모 노드가 나의 다음으로 큰놈임
// 만약 내가 부모 노드의 오른쪽 자식이면 계속 계층을 올라가면서
// 부모 노드의 오른쪽 노드가 새로운 경로라서 즉, 내가 왼쪽 자식 노드가 될때까지
// 타고 올라가고 그러면 내가 왼쪽 자식 노드니까 그 때의 부모노드가 다음으로 큰 놈임
while (parent && node == parent->right)
{
node = parent;
parent = parent->parent;
}
// 근데 만약에 더 큰 놈이 없으면 루트 노드까지 올라간다음에 한 번 더 올라가서
// nullptr 인 NodeTree* 가 반환 될 거임.
return parent;
}
void BinarySearchTree::Insert(int key)
{
NodeTree* newNode = new NodeTree();
newNode->key = key;
if (_root == nullptr)
{
_root = newNode;
return;
}
NodeTree* node = _root;
NodeTree* parent = nullptr;
while (node)
{
// 해당 구문이 처음에 나옴으로써
// 들어가야할 노드 자리의 부모 노드 자리를 알게 된다.
// 이진 탐색 트리로 insert 하면 무조건 한 경로의 마지막까지 내려가게
// 되어 있다.
parent = node;
// 여기서 공노드 나올때가지 계속 비교하고 밑에서는 대입을 하는 거임
if (key < node->key)
node = node->left;
else
node = node->right;
}
// 완전히 추가 될 노드 이므로 위에서 구한
// parent 를 부모로 받고 마지막으로 한 번 더 비교해서
// 왼/오 결정해서 거기 들어간다.
newNode->parent = parent;
if (key < parent->key)
{
parent->left = newNode;
}
else
parent-> right = newNode;
}
void BinarySearchTree::Delete(int key)
{
NodeTree* deleteNode = Search(_root, key);
Delete(deleteNode);
}
void BinarySearchTree::Delete(NodeTree* node)
{
// 뭔가 문제가 있음
if (node == nullptr)
return;
// child 가 하나만 있거나 아예 없거나 를 예상 가능
if (node->left == nullptr)
{
// Replace 가 child 가 전부 null 이어도 상관 없게 코드되어있음
Replace(node, node->right);
}
else if (node->right == nullptr)
Replace(node, node->left);
// 둘 다 있을 때
else
{
NodeTree* next = Next(node);
// 삭제할 노드를 삭제하는게 아니라 사실상
// 데이터만 삭제할 노드 보다 다음으로 큰 next 의 데이터로
// 바꿔치기 함으로써 마치 삭제한 것 처럼 보이게 함
// 그 후 next 노드는 바꿔치기를 당했으니 이제 필요 없음 실제로 삭제
// 당연히 삭제는 자식 노드를 끌어오거나 없으면 null로 밀어버리느거
node->key = next->key;
// 재귀로 반복해서 바꿔치기해서 자식이 null 일 때까지 반복
// null 이면 null 로 밀어버릴거임
Delete(next);
}
}
// u 서브트리를 v 서브트리로 교체
// 간선 바꿔치기 한다. 연결점을
// 그리고 delete u
void BinarySearchTree::Replace(NodeTree* u, NodeTree* v)
{
// u 의 parent 가 null 이면 u 가 루트라는거니깐
// _root = v;
if (u->parent == nullptr)
_root = v;
// u 가 부모 노드의 왼쪽 자식 일 때
else if (u == u->parent->left)
{
u->parent->left = v;
}
else
{
u->parent->right = v;
}
// 만약 자식 없는 애를 없앨때는 nullptr NodeTree 로 밀어버림
// 그래서 null 로 넣는것도 호환되게 v 의 null 체크해서
// null 이 아닐 때만 해당 코드 실행하게 하자
if (v)
v->parent = u->parent;
delete u;
}
'자료구조 알고리즘' 카테고리의 다른 글
| 길찾기 1 우수법 (0) | 2024.05.29 |
|---|---|
| 레드 블랙 트리 (1) | 2024.05.29 |
| 힙으로 구현한 우선순위 큐 (0) | 2024.05.29 |
| 이진트리 와 힙 이론 (0) | 2024.05.29 |
| 트리 (0) | 2024.05.29 |

